Готовые графики функций. Построение графиков онлайн. Графики и основные свойства элементарных функций

Национальный научно-исследовательский университет

Кафедра прикладной геологии

Реферат по высшей математике

На тему: «Основные элементарные функции,

их свойства и графики»

Выполнил:

Проверил:

преподаватель

Определение. Функция, заданная формулой у=а х (где а>0, а≠1), называется показательной функцией с основанием а.

Сформулируем основные свойства показательной функции:

1. Область определения - множество (R) всех действительных чисел.

2. Область значений - множество (R+) всех положительных действительных чисел.

3. При а > 1 функция возрастает на всей числовой прямой; при 0<а<1 функция убывает.

4. Является функцией общего вида.

, на интервале xÎ [-3;3] , на интервале xÎ [-3;3]

Функция вида у(х)=х n , где n – число ÎR, называется степенной функцией. Число n может принимать раличные значения: как целые, так и дробные, как четные, так и нечетные. В зависимости от этого, степенная функция будет иметь разный вид. Рассмотрим частные случаи, которые являются степенными функциями и отражают основные свойства данного вида кривых в следующем порядке: степенная функция у=х² (функция с четным показателем степени – парабола), степенная функция у=х³ (функция с нечетным показателем степени – кубическая парабола) и функция у=√х (х в степени ½) (функция с дробным показателем степени), функция с отрицательным целым показателем (гипербола).

Степенная функция у=х²

1. D(x)=R – функция определена на все числовой оси;

2. E(y)= и возрастает на промежутке

Степенная функция у=х³

1. График функции у=х³ называется кубической параболой. Степенная функция у=х³ обладает следующими свойствами:

2. D(x)=R – функция определена на все числовой оси;

3. E(y)=(-∞;∞) – функция принимает все значения на своей области определения;

4. При х=0 у=0 – функция проходит через начало координат O(0;0).

5. Функция возрастает на всей области определения.

6. Функция является нечетной (симметрична относительно начала координат).

, на интервале xÎ [-3;3]

В зависимости от числового множителя, стоящего перед х³, функция может быть крутой/пологой и возрастать/убывать.

Степенная функция с целым отрицательным показателем:

Если показатель степени n является нечетным, то график такой степенной функции называется гиперболой. Степенная функция с целым отрицательным показателем степени обладает следующими свойствами:

1. D(x)=(-∞;0)U(0;∞) для любого n;

2. E(y)=(-∞;0)U(0;∞), если n – нечетное число; E(y)=(0;∞), если n – четное число;

3. Функция убывает на всей области определения, если n – нечетное число; функция возрастает на промежутке (-∞;0) и убывает на промежутке (0;∞), если n – четное число.

4. Функция является нечетной (симметрична относительно начала координат), если n – нечетное число; функция является четной, если n – четное число.

5. Функция проходит через точки (1;1) и (-1;-1), если n – нечетное число и через точки (1;1) и (-1;1), если n – четное число.

, на интервале xÎ [-3;3]

Степенная функция с дробным показателем

Степенная функция с дробным показателем вида (картинка) имеет график функции, изображенный на рисунке. Степенная функция с дробным показателем степени обладает следующими свойствами: (картинка)

1. D(x) ÎR, если n – нечетное число и D(x)= , на интервале xÎ , на интервале xÎ [-3;3]

Логарифмическая функция у = log a x обладает следующими свойствами:

1. Область определения D(x)Î (0; + ∞).

2. Область значений E(y) Î (- ∞; + ∞)

3. Функция ни четная, ни нечетная (общего вида).

4. Функция возрастает на промежутке (0; + ∞) при a > 1, убывает на (0; + ∞) при 0 < а < 1.

График функции у = log a x может быть получен из графика функции у = а х с помощью преобразования симметрии относительно прямой у = х. На рисунке 9 построен график логарифмической функции для а > 1, а на рисунке 10 - для 0 < a < 1.

; на интервале xÎ ; на интервале xÎ

Функции y = sin х, у = cos х, у = tg х, у = ctg х называют тригонометрическими функциями.

Функции у = sin х, у = tg х, у = ctg х нечетные, а функция у = соs х четная.

Функция y = sin (х).

1. Область определения D(x) ÎR.

2. Область значений E(y) Î [ - 1; 1].

3. Функция периодическая; основной период равен 2π.

4. Функция нечетная.

5. Функция возрастает на промежутках [ -π/2 + 2πn; π/2 + 2πn] и убывает на промежутках [ π/2 + 2πn; 3π/2 + 2πn], n Î Z.

График функции у = sin (х) изображен на рисунке 11.

Степенная функция. Это функция: y = ax n , где a, n – постоянные. При n = 1 получаем прямую пропорциональность : y = ax ; при n = 2 - квадратную параболу ; при n = - 1 - обратную пропорциональность или гиперболу . Таким образом, эти функции - частные случаи степенной функции. Мы знаем, что нулевая степень любого числа, отличного от нуля, равна 1, cледовательно, приn = 0 степенная функция превращается в постоянную величину: y = a , т. e . её график - прямая линия, параллельная оси Х , исключая начало координат (поясните, пожалуйста, почему ? ). Все эти случаи (при a = 1 ) показаны на рис.13 (n 0 ) и рис.14 ( n < 0). Отрицательные значения x здесь не рассматриваются, так как тогда некоторые функции:

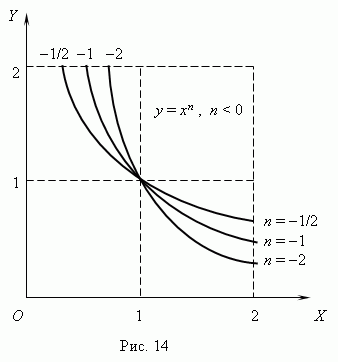
Если n – целые, степенные функции имеют смысл и при x < 0, но их графики имеют различный вид в зависимости от того, является ли n чётным числом или нечётным. На рис.15 показаны две такие степенные функции: для n = 2 и n = 3.


При n = 2 функция чётная и её график симметричен относительно оси Y . При n = 3 функция нечётная и её график симметричен относительно начала координат. Функция y = x 3 называется кубической параболой .

На рис.16 представлена функция . Эта функция является обратной к квадратной параболе y = x 2 , её график получается поворотом графика квадратной параболы вокруг биссектрисы 1-го координатного угла . Это способ получения графика любой обратной функции из графика её исходной функции. Мы видим по графику, что это двузначная функция (об этом говорит и знак ± перед квадратным корнем). Такие функции не изучаются в элементарной математике, поэтому в качестве функции мы рассматриваем обычно одну из её ветвей: верхнюю или нижнюю.

Линейной функцией называется функция вида y=kx+b, где x-независимая переменная, k и b-любые числа.
Графиком линейной функции является прямая.

1. Чтобы постороить график функции, нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y.

Например, чтобы построить график функции y= ⅓ x+2, удобно взять x=0 и x=3, тогда ординаты эти точек будут равны y=2 и y=3. Получим точки А(0;2) и В(3;3). Соединим их и получим график функции y= ⅓ x+2:

2. В формуле y=kx+b число k называется коэффицентом пропорциональности:
если k>0, то функция y=kx+b возрастает
если k
Коэффициент b показывает смещение графика функции вдоль оси OY:
если b>0, то график функции y=kx+b получается из графика функцииy=kx сдвигом на b единиц вверх вдоль оси OY
если b
На рисунке ниже изображены графики функций y=2x+3; y= ½ x+3; y=x+3

Заметим, что во всех этих функциях коэффициент k больше нуля, и функции являются возрастающими. Причем, чем больше значение k, тем больше угол наклона прямой к положительному направлению оси OX.

Во всех функциях b=3 – и мы видим, что все графики пересекают ось OY в точке (0;3)

Теперь рассмотрим графики функций y=-2x+3; y=- ½ x+3; y=-x+3

На этот раз во всех функциях коэффициент k меньше нуля, и функции убывают. Коэффициент b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)

Рассмотрим графики функций y=2x+3; y=2x; y=2x-3

Теперь во всех уравнениях функций коэффициенты k равны 2. И мы получили три параллельные прямые.

Но коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
График функции y=2x+3 (b=3) пересекает ось OY в точке (0;3)
График функции y=2x (b=0) пересекает ось OY в точке (0;0) - начале координат.
График функции y=2x-3 (b=-3) пересекает ось OY в точке (0;-3)

Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции y=kx+b.
Если k 0

Если k>0 и b>0 , то график функции y=kx+b имеет вид:

Если k>0 и b , то график функции y=kx+b имеет вид:

Если k, то график функции y=kx+b имеет вид:

Если k=0 , то функция y=kx+b превращается в функцию y=b и ее график имеет вид:

Ординаты всех точек графика функции y=b равны b Если b=0 , то график функции y=kx (прямая пропорциональность) проходит через начало координат:

3. Отдельно отметим график уравнения x=a. График этого уравнения представляет собой прямую линию, параллельую оси OY все точки которой имеют абсциссу x=a.

Например, график уравнения x=3 выглядит так:
Внимание! Уравнение x=a не является функцией, так одному значению аргумента соотвутствуют разные значения функции, что не соответствует определению функции.

4. Условие параллельности двух прямых:

График функции y=k 1 x+b 1 параллелен графику функции y=k 2 x+b 2 , если k 1 =k 2

5. Условие перепендикулярности двух прямых:

График функции y=k 1 x+b 1 перепендикулярен графику функции y=k 2 x+b 2 , если k 1 *k 2 =-1 или k 1 =-1/k 2

6. Точки пересечения графика функции y=kx+b с осями координат.

С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).

С осью ОХ: Ордината любой точки, принадлежащей оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ нужно в уравнение функции вместо y подставить ноль. Получим 0=kx+b. Отсюда x=-b/k. То есть точка пересечения с осью OX имеет координаты (-b/k;0):

Основные элементарные функции, присущие им свойства и соответствующие графики – одни из азов математических знаний, схожих по степени важности с таблицей умножения. Элементарные функции являются базой, опорой для изучения всех теоретических вопросов.

Статья ниже дает ключевой материал по теме основных элементарных функций. Мы введем термины, дадим им определения; подробно изучим каждый вид элементарных функций, разберем их свойства.

Выделяют следующие виды основных элементарных функций:

Определение 1

• постоянная функция (константа);
• корень n -ой степени;
• степенная функция;
• показательная функция;
• логарифмическая функция;
• тригонометрические функции;
• братные тригонометрические функции.

Постоянная функция определяется формулой: y = C (C – некое действительное число) и имеет также название: константа. Данная функция определяет соответствие любому действительному значению независимой переменной x одного и того же значения переменной y – значение C .

График константы – это прямая, которая параллельна оси абсцисс и проходит через точку, имеющую координаты (0 , С) . Для наглядности приведем графики постоянных функций y = 5 , y = - 2 , y = 3 , y = 3 (на чертеже обозначено черным, красным и синим цветами соответственно).

Определение 2

Данная элементарная функция определяется формулой y = x n (n – натуральное число больше единицы).

Рассмотрим две вариации функции.

1. Корень n -й степени, n – четное число

Для наглядности укажем чертеж, на котором изображены графики таких функций: y = x , y = x 4 и y = x 8 . Эти функции отмечены цветом: черный, красный и синий соответственно.

Похожий вид у графиков функции четной степени при иных значениях показателя.

Определение 3

Свойства функции корень n-ой степени, n – четное число

• область определения – множество всех неотрицательных действительных чисел [ 0 , + ∞) ;
• когда x = 0 , функция y = x n имеет значение, равное нулю;
• данная функция- функция общего вида (не является ни четной, ни нечетной);
• область значений: [ 0 , + ∞) ;
• данная функция y = x n при четных показателях корня возрастает на всей области определения;
• функция обладает выпуклостью с направлением вверх на всей области определения;
• отсутствуют точки перегиба;
• асимптоты отсутствуют;
• график функции при четных n проходит через точки (0 ; 0) и (1 ; 1) .

1. Корень n -й степени, n – нечетное число

Такая функция определена на всем множестве действительных чисел. Для наглядности рассмотрим графики функций y = x 3 , y = x 5 и x 9 . На чертеже они обозначены цветами: черный, красный и синий цвета кривых соответственно.

Иные нечетные значения показателя корня функции y = x n дадут график аналогичного вида.

Определение 4

Свойства функции корень n-ой степени, n – нечетное число

• область определения – множество всех действительных чисел;
• данная функция – нечетная;
• область значений – множество всех действительных чисел;
• функция y = x n при нечетных показателях корня возрастает на всей области определения;
• функция имеет вогнутость на промежутке (- ∞ ; 0 ] и выпуклость на промежутке [ 0 , + ∞) ;
• точка перегиба имеет координаты (0 ; 0) ;
• асимптоты отсутствуют;
• график функции при нечетных n проходит через точки (- 1 ; - 1) , (0 ; 0) и (1 ; 1) .

Степенная функция

Определение 5

Степенная функция определяется формулой y = x a .

Вид графиков и свойства функции зависят от значения показателя степени.

• когда степенная функция имеет целый показатель a , то вид графика степенной функции и ее свойства зависят от того, четный или нечетный показатель степени, а также того, какой знак имеет показатель степени. Рассмотрим все эти частные случаи подробнее ниже;
• показатель степени может быть дробным или иррациональным – в зависимости от этого также варьируется вид графиков и свойства функции. Мы разберем частные случаи, задав несколько условий: 0 < a < 1 ; a > 1 ; - 1 < a < 0 и a < - 1 ;
• степенная функция может иметь нулевой показатель, этот случай также ниже разберем подробнее.

Разберем степенную функцию y = x a , когда a – нечетное положительное число, например, a = 1 , 3 , 5 …

Для наглядности укажем графики таких степенных функций: y = x (черный цвет графика), y = x 3 (синий цвет графика), y = x 5 (красный цвет графика), y = x 7 (зеленый цвет графика). Когда a = 1 , получаем линейную функцию y = x .

Определение 6

Свойства степенной функции, когда показатель степени – нечетный положительный

• функция является возрастающей при x ∈ (- ∞ ; + ∞) ;
• функция имеет выпуклость при x ∈ (- ∞ ; 0 ] и вогнутость при x ∈ [ 0 ; + ∞) (исключая линейную функцию);
• точка перегиба имеет координаты (0 ; 0) (исключая линейную функцию);
• асимптоты отсутствуют;
• точки прохождения функции: (- 1 ; - 1) , (0 ; 0) , (1 ; 1) .

Разберем степенную функцию y = x a , когда a – четное положительное число, например, a = 2 , 4 , 6 …

Для наглядности укажем графики таких степенных функций: y = x 2 (черный цвет графика), y = x 4 (синий цвет графика), y = x 8 (красный цвет графика). Когда a = 2 , получаем квадратичную функцию, график которой – квадратичная парабола.

Определение 7

Свойства степенной функции, когда показатель степени – четный положительный:

• область определения: x ∈ (- ∞ ; + ∞) ;
• убывающей при x ∈ (- ∞ ; 0 ] ;
• функция имеет вогнутость при x ∈ (- ∞ ; + ∞) ;
• очки перегиба отсутствуют;
• асимптоты отсутствуют;
• точки прохождения функции: (- 1 ; 1) , (0 ; 0) , (1 ; 1) .

На рисунке ниже приведены примеры графиков степенной функции y = x a , когда a – нечетное отрицательное число: y = x - 9 (черный цвет графика); y = x - 5 (синий цвет графика); y = x - 3 (красный цвет графика); y = x - 1 (зеленый цвет графика). Когда a = - 1 , получаем обратную пропорциональность, график которой – гипербола.

Определение 8

Свойства степенной функции, когда показатель степени – нечетный отрицательный:

Когда х = 0 , получаем разрыв второго рода, поскольку lim x → 0 - 0 x a = - ∞ , lim x → 0 + 0 x a = + ∞ при a = - 1 , - 3 , - 5 , … . Таким образом, прямая х = 0 – вертикальная асимптота;

• область значений: y ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;
• функция является нечетной, поскольку y (- x) = - y (x) ;
• функция является убывающей при x ∈ - ∞ ; 0 ∪ (0 ; + ∞) ;
• функция имеет выпуклость при x ∈ (- ∞ ; 0) и вогнутость при x ∈ (0 ; + ∞) ;
• точки перегиба отсутствуют;

k = lim x → ∞ x a x = 0 , b = lim x → ∞ (x a - k x) = 0 ⇒ y = k x + b = 0 , когда а = - 1 , - 3 , - 5 , . . . .

• точки прохождения функции: (- 1 ; - 1) , (1 ; 1) .

На рисунке ниже приведены примеры графиков степенной функции y = x a , когда a – четное отрицательное число: y = x - 8 (черный цвет графика); y = x - 4 (синий цвет графика); y = x - 2 (красный цвет графика).

Определение 9

Свойства степенной функции, когда показатель степени – четный отрицательный:

• область определения: x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;

Когда х = 0 , получаем разрыв второго рода, поскольку lim x → 0 - 0 x a = + ∞ , lim x → 0 + 0 x a = + ∞ при a = - 2 , - 4 , - 6 , … . Таким образом, прямая х = 0 – вертикальная асимптота;

• функция является четной, поскольку y (- x) = y (x) ;
• функция является возрастающей при x ∈ (- ∞ ; 0) и убывающей при x ∈ 0 ; + ∞ ;
• функция имеет вогнутость при x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;
• точки перегиба отсутствуют;
• горизонтальная асимптота – прямая y = 0 , поскольку:

k = lim x → ∞ x a x = 0 , b = lim x → ∞ (x a - k x) = 0 ⇒ y = k x + b = 0 , когда a = - 2 , - 4 , - 6 , . . . .

• точки прохождения функции: (- 1 ; 1) , (1 ; 1) .

С самого начала обратите внимание на следующий аспект: в случае, когда a – положительная дробь с нечетным знаменателем, некоторые авторы принимают за область определения этой степенной функции интервал - ∞ ; + ∞ , оговаривая при этом, что показатель a – несократимая дробь. На данный момент авторы многих учебных изданий по алгебре и началам анализа НЕ ОПРЕДЕЛЯЮТ степенные функции, где показатель – дробь с нечетным знаменателем при отрицательных значениях аргумента. Далее мы придержемся именно такой позиции: возьмем за область определения степенных функций с дробными положительными показателями степени множество [ 0 ; + ∞) . Рекомендация для учащихся: выяснить взгляд преподавателя на этот момент во избежание разногласий.

Итак, разберем степенную функцию y = x a , когда показатель степени – рациональное или иррациональное число при условии, что 0 < a < 1 .

Проиллюстрируем графиками степенные функции y = x a , когда a = 11 12 (черный цвет графика); a = 5 7 (красный цвет графика); a = 1 3 (синий цвет графика); a = 2 5 (зеленый цвет графика).

Иные значения показателя степени a (при условии 0 < a < 1) дадут аналогичный вид графика.

Определение 10

Свойства степенной функции при 0 < a < 1:

• область значений: y ∈ [ 0 ; + ∞) ;
• функция является возрастающей при x ∈ [ 0 ; + ∞) ;
• функция имеет выпуклость при x ∈ (0 ; + ∞) ;
• точки перегиба отсутствуют;
• асимптоты отсутствуют;

Разберем степенную функцию y = x a , когда показатель степени – нецелое рациональное или иррациональное число при условии, что a > 1 .

Проиллюстрируем графиками степенную функцию y = x a в заданных условиях на примере таких функций: y = x 5 4 , y = x 4 3 , y = x 7 3 , y = x 3 π (черный, красный, синий, зеленый цвет графиков соответственно).

Иные значения показателя степени а при условии a > 1 дадут похожий вид графика.

Определение 11

Свойства степенной функции при a > 1:

• область определения: x ∈ [ 0 ; + ∞) ;
• область значений: y ∈ [ 0 ; + ∞) ;
• данная функция – функция общего вида (не является ни нечетной, ни четной);
• функция является возрастающей при x ∈ [ 0 ; + ∞) ;
• функция имеет вогнутость при x ∈ (0 ; + ∞) (когда 1 < a < 2) и выпуклость при x ∈ [ 0 ; + ∞) (когда a > 2);
• точки перегиба отсутствуют;
• асимптоты отсутствуют;
• точки прохождения функции: (0 ; 0) , (1 ; 1) .

Обращаем ваше внимание!Когда a – отрицательная дробь с нечетным знаменателем, в работах некоторых авторов встречается взгляд, что область определения в данном случае – интервал - ∞ ; 0 ∪ (0 ; + ∞) с оговоркой, что показатель степени a – несократимая дробь. На данный момент авторы учебных материалов по алгебре и началам анализа НЕ ОПРЕДЕЛЯЮТ степенные функции с показателем в виде дроби с нечетным знаменателем при отрицательных значениях аргумента. Далее мы придерживаемся именно такого взгляда: возьмем за область определения степенных функций с дробными отрицательными показателями множество (0 ; + ∞) . Рекомендация для учащихся: уточните видение вашего преподавателя на этот момент во избежание разногласий.

Продолжаем тему и разбираем степенную функцию y = x a при условии: - 1 < a < 0 .

Приведем чертеж графиков следующий функций: y = x - 5 6 , y = x - 2 3 , y = x - 1 2 2 , y = x - 1 7 (черный, красный, синий, зеленый цвет линий соответственно).

Определение 12

Свойства степенной функции при - 1 < a < 0:

lim x → 0 + 0 x a = + ∞ , когда - 1 < a < 0 , т.е. х = 0 – вертикальная асимптота;

• область значений: y ∈ 0 ; + ∞ ;
• данная функция – функция общего вида (не является ни нечетной, ни четной);
• точки перегиба отсутствуют;

На чертеже ниже приведены графики степенных функций y = x - 5 4 , y = x - 5 3 , y = x - 6 , y = x - 24 7 (черный, красный, синий, зеленый цвета кривых соответственно).

Определение 13

Свойства степенной функции при a < - 1:

• область определения: x ∈ 0 ; + ∞ ;

lim x → 0 + 0 x a = + ∞ , когда a < - 1 , т.е. х = 0 – вертикальная асимптота;

• область значений: y ∈ (0 ; + ∞) ;
• данная функция – функция общего вида (не является ни нечетной, ни четной);
• функция является убывающей при x ∈ 0 ; + ∞ ;
• функция имеет вогнутость при x ∈ 0 ; + ∞ ;
• точки перегиба отсутствуют;
• горизонтальная асимптота – прямая y = 0 ;
• точка прохождения функции: (1 ; 1) .

Когда a = 0 и х ≠ 0 , получим функцию y = x 0 = 1 , определяющую прямую, из которой исключена точка (0 ; 1) (условились, что выражению 0 0 не будет придаваться никакого значения).

Показательная функция имеет вид y = a x , где а > 0 и а ≠ 1 , и график этой функции выглядит различно, исходя из значения основания a . Рассмотрим частные случаи.

Сначала разберем ситуацию, когда основание показательной функции имеет значение от нуля до единицы (0 < a < 1) . Наглядным примером послужат графики функций при a = 1 2 (синий цвет кривой) и a = 5 6 (красный цвет кривой).

Подобный же вид будут иметь графики показательной функции при иных значениях основания при условии 0 < a < 1 .

Определение 14

Свойства показательной функции, когда основание меньше единицы:

• область значений: y ∈ (0 ; + ∞) ;
• данная функция – функция общего вида (не является ни нечетной, ни четной);
• показательная функция, у которой основание меньше единицы, является убывающей на всей области определения;
• точки перегиба отсутствуют;
• горизонтальная асимптота – прямая y = 0 при переменной x , стремящейся к + ∞ ;

Теперь рассмотрим случай, когда основание показательной функции больше, чем единица (а > 1) .

Проиллюстрируем этот частный случай графиком показательных функций y = 3 2 x (синий цвет кривой) и y = e x (красный цвет графика).

Иные значения основания, большие единицы, дадут аналогичный вид графика показательной функции.

Определение 15

Свойства показательной функции, когда основание больше единицы:

• область определения – все множество действительных чисел;
• область значений: y ∈ (0 ; + ∞) ;
• данная функция – функция общего вида (не является ни нечетной, ни четной);
• показательная функция, у которой основание больше единицы, является возрастающей при x ∈ - ∞ ; + ∞ ;
• функция имеет вогнутость при x ∈ - ∞ ; + ∞ ;
• точки перегиба отсутствуют;
• горизонтальная асимптота – прямая y = 0 при переменной x , стремящейся к - ∞ ;
• точка прохождения функции: (0 ; 1) .

Логарифмическая функция имеет вид y = log a (x) , где a > 0 , a ≠ 1 .

Такая функция определена только при положительных значениях аргумента: при x ∈ 0 ; + ∞ .

График логарифмической функции имеет различный вид, исходя из значения основания а.

Рассмотрим сначала ситуацию, когда 0 < a < 1 . Продемонстрируем этот частный случай графиком логарифмической функции при a = 1 2 (синий цвет кривой) и а = 5 6 (красный цвет кривой).

Иные значения основания, не большие единицы, дадут аналогичный вид графика.

Определение 16

Свойства логарифмической функции, когда основание меньше единицы:

• область определения: x ∈ 0 ; + ∞ . Когда х стремится к нулю справа, значения функции стремятся к + ∞ ;
• область значений: y ∈ - ∞ ; + ∞ ;
• данная функция – функция общего вида (не является ни нечетной, ни четной);
• логарифмическая
• функция имеет вогнутость при x ∈ 0 ; + ∞ ;
• точки перегиба отсутствуют;
• асимптоты отсутствуют;

Теперь разберем частный случай, когда основание логарифмической функции больше единицы: а > 1 . На чертеже ниже –графики логарифмических функций y = log 3 2 x и y = ln x (синий и красный цвета графиков соответственно).

Иные значения основания больше единицы дадут аналогичный вид графика.

Определение 17

Свойства логарифмической функции, когда основание больше единицы:

• область определения: x ∈ 0 ; + ∞ . Когда х стремится к нулю справа, значения функции стремятся к - ∞ ;
• область значений: y ∈ - ∞ ; + ∞ (все множество действительных чисел);
• данная функция – функция общего вида (не является ни нечетной, ни четной);
• логарифмическая функция является возрастающей при x ∈ 0 ; + ∞ ;
• функция имеет выпуклость при x ∈ 0 ; + ∞ ;
• точки перегиба отсутствуют;
• асимптоты отсутствуют;
• точка прохождения функции: (1 ; 0) .

Тригонометрические функции – это синус, косинус, тангенс и котангенс. Разберем свойства каждой из них и соответствующие графики.

В общем для всех тригонометрических функций характерно свойство периодичности, т.е. когда значения функций повторяются при разных значениях аргумента, отличающихся друг от друга на величину периода f (x + T) = f (x) (T – период). Таким образом, в списке свойств тригонометрических функций добавляется пункт «наименьший положительный период». Помимо этого, будем указывать такие значения аргумента, при которых соответствующая функция обращается в нуль.

1. Функция синус: y = sin (х)

График данной функции называется синусоида.

Определение 18

Свойства функции синус:

• область определения: все множество действительных чисел x ∈ - ∞ ; + ∞ ;
• функция обращается в нуль, когда x = π · k , где k ∈ Z (Z – множество целых чисел);
• функция является возрастающей при x ∈ - π 2 + 2 π · k ; π 2 + 2 π · k , k ∈ Z и убывающей при x ∈ π 2 + 2 π · k ; 3 π 2 + 2 π · k , k ∈ Z ;
• функция синус имеет локальные максимумы в точках π 2 + 2 π · k ; 1 и локальные минимумы в точках - π 2 + 2 π · k ; - 1 , k ∈ Z ;
• функция синус вогнутая, когда x ∈ - π + 2 π · k ; 2 π · k , k ∈ Z и выпуклая, когда x ∈ 2 π · k ; π + 2 π · k , k ∈ Z ;
• асимптоты отсутствуют.

1. Функция косинус: y = cos (х)

График данной функции называется косинусоида.

Определение 19

Свойства функции косинус:

• область определения: x ∈ - ∞ ; + ∞ ;
• наименьший положительный период: Т = 2 π ;
• область значений: y ∈ - 1 ; 1 ;
• данная функция – четная, поскольку y (- x) = y (x) ;
• функция является возрастающей при x ∈ - π + 2 π · k ; 2 π · k , k ∈ Z и убывающей при x ∈ 2 π · k ; π + 2 π · k , k ∈ Z ;
• функция косинус имеет локальные максимумы в точках 2 π · k ; 1 , k ∈ Z и локальные минимумы в точках π + 2 π · k ; - 1 , k ∈ z ;
• функция косинус вогнутая, когда x ∈ π 2 + 2 π · k ; 3 π 2 + 2 π · k , k ∈ Z и выпуклая, когда x ∈ - π 2 + 2 π · k ; π 2 + 2 π · k , k ∈ Z ;
• точки перегиба имеют координаты π 2 + π · k ; 0 , k ∈ Z
• асимптоты отсутствуют.

1. Функция тангенс: y = t g (х)

График данной функции называется тангенсоида.

Определение 20

Свойства функции тангенс:

• область определения: x ∈ - π 2 + π · k ; π 2 + π · k , где k ∈ Z (Z – множество целых чисел);
• Поведение функции тангенс на границе области определения lim x → π 2 + π · k + 0 t g (x) = - ∞ , lim x → π 2 + π · k - 0 t g (x) = + ∞ . Таким образом, прямые x = π 2 + π · k k ∈ Z – вертикальные асимптоты;
• функция обращается в нуль, когда x = π · k при k ∈ Z (Z – множество целых чисел);
• область значений: y ∈ - ∞ ; + ∞ ;
• данная функция – нечетная, поскольку y (- x) = - y (x) ;
• функция является возрастающей при - π 2 + π · k ; π 2 + π · k , k ∈ Z ;
• функция тангенс является вогнутой при x ∈ [ π · k ; π 2 + π · k) , k ∈ Z и выпуклой при x ∈ (- π 2 + π · k ; π · k ] , k ∈ Z ;
• точки перегиба имеют координаты π · k ; 0 , k ∈ Z ;

1. Функция котангенс: y = c t g (х)

График данной функции называется котангенсоида.

Определение 21

Свойства функции котангенс:

• область определения: x ∈ (π · k ; π + π · k) , где k ∈ Z (Z – множество целых чисел);

Поведение функции котангенс на границе области определения lim x → π · k + 0 t g (x) = + ∞ , lim x → π · k - 0 t g (x) = - ∞ . Таким образом, прямые x = π · k k ∈ Z – вертикальные асимптоты;

• наименьший положительный период: Т = π ;
• функция обращается в нуль, когда x = π 2 + π · k при k ∈ Z (Z – множество целых чисел);
• область значений: y ∈ - ∞ ; + ∞ ;
• данная функция – нечетная, поскольку y (- x) = - y (x) ;
• функция является убывающей при x ∈ π · k ; π + π · k , k ∈ Z ;
• функция котангенс является вогнутой при x ∈ (π · k ; π 2 + π · k ] , k ∈ Z и выпуклой при x ∈ [ - π 2 + π · k ; π · k) , k ∈ Z ;
• точки перегиба имеют координаты π 2 + π · k ; 0 , k ∈ Z ;
• наклонные и горизонтальные асимптоты отсутствуют.

Обратные тригонометрические функции – это арксинус, арккосинус, арктангенс и арккотангенс. Зачастую, в связи с наличием приставки «арк» в названии, обратные тригонометрические функции называют аркфункциями.

1. Функция арксинус: y = a r c sin (х)

Определение 22

Свойства функции арксинус:

• данная функция – нечетная, поскольку y (- x) = - y (x) ;
• функция арксинус имеет вогнутость при x ∈ 0 ; 1 и выпуклость при x ∈ - 1 ; 0 ;
• точки перегиба имеют координаты (0 ; 0) , она же – нуль функции;
• асимптоты отсутствуют.

1. Функция арккосинус: y = a r c cos (х)

Определение 23

Свойства функции арккосинус:

• область определения: x ∈ - 1 ; 1 ;
• область значений: y ∈ 0 ; π ;
• данная функция - общего вида (ни четная, ни нечетная);
• функция является убывающей на всей области определения;
• функция арккосинус имеет вогнутость при x ∈ - 1 ; 0 и выпуклость при x ∈ 0 ; 1 ;
• точки перегиба имеют координаты 0 ; π 2 ;
• асимптоты отсутствуют.

1. Функция арктангенс: y = a r c t g (х)

Определение 24

Свойства функции арктангенс:

• область определения: x ∈ - ∞ ; + ∞ ;
• область значений: y ∈ - π 2 ; π 2 ;
• данная функция – нечетная, поскольку y (- x) = - y (x) ;
• функция является возрастающей на всей области определения;
• функция арктангенс имеет вогнутость при x ∈ (- ∞ ; 0 ] и выпуклость при x ∈ [ 0 ; + ∞) ;
• точка перегиба имеет координаты (0 ; 0) , она же – нуль функции;
• горизонтальные асимптоты – прямые y = - π 2 при x → - ∞ и y = π 2 при x → + ∞ (на рисунке асимптоты – это линии зеленого цвета).

1. Функция арккотангенс: y = a r c c t g (х)

Определение 25

Свойства функции арккотангенс:

• область определения: x ∈ - ∞ ; + ∞ ;
• область значений: y ∈ (0 ; π) ;
• данная функция – общего вида;
• функция является убывающей на всей области определения;
• функция арккотангенс имеет вогнутость при x ∈ [ 0 ; + ∞) и выпуклость при x ∈ (- ∞ ; 0 ] ;
• точка перегиба имеет координаты 0 ; π 2 ;
• горизонтальные асимптоты – прямые y = π при x → - ∞ (на чертеже – линия зеленого цвета) и y = 0 при x → + ∞ .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter